1、直线与方程
(1)直线的倾斜角
概念:x轴正向与直线向上方向之间所成的角叫直线的倾斜角。特别地,当直线与x轴平行或重合时,大家规定它的倾斜角为0度。因此,倾斜角的取值范围是0180
(2)直线的斜率
①概念:倾斜角不是90的直线,它的倾斜角的正切叫做这条直线的斜率。直线的斜率常用k表示。即。斜率反映直线与轴的倾斜程度。当时,。当时,;当时,没有。
②过两点的直线的斜率公式:
注意下面四点:(1)当时,公式右侧无意义,直线的斜率没有,倾斜角为90
(2)k与P1、P2的顺序无关;
(3)将来求斜率可不通过倾斜角而由直线上两点的坐标直接求得;
(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。
(3)直线方程
①点斜式:直线斜率k,且过点
注意:当直线的斜率为0时,k=0,直线的方程是y=y1。当直线的斜率为90时,直线的斜率没有,它的方程不可以用点斜式表示.但因l上每一点的横坐标都等于x1,所以它的方程是x=x1。
②斜截式:,直线斜率为k,直线在y轴上的截距为b
③两点式:()直线两点,
④截矩式:其中直线与轴交于点,与轴交于点,即与轴、轴的截距分别为。
⑤一般式:(A,B不全为0)
⑤一般式:(A,B不全为0)
注意:
1.各式的适用范围
2.特殊的方程如:平行于x轴的直线:(b为常数);平行于y轴的直线:(a为常数);
(4)直线系方程:即具备某一一同性质的直线
(一)平行直线系
平行于已知直线(是不全为0的常数)的直线系:(C为常数)
(二)过定点的直线系
(ⅰ)斜率为k的直线系:,直线过定点;
(ⅱ)过两条直线,的交点的直线系方程为(为参数),其中直线不在直线系中。
(5)两直线平行与垂直
当,时,;注意:借助斜率判断直线的平行与垂直时,应该注意斜率的存在与否。
(6)两条直线的交点
相交:交点坐标即方程组的一组解。方程组无解;方程组有无数解与重合
(7)两点间距离公式:设是平面直角坐标系中的两个点,则
(8)点到直线距离公式:一点到直线的距离
(9)两平行直线距离公式:在任一直线上任取一点,再转化为点到直线的距离进行求解。
高中数学要点1、直线方程的一般式关于x和y的一次方程都表示一条直线.大家把方程写为Ax+By+C=0,这个方程(其中A、B不全为零)叫做直线方程的一般式.
高中数学要点2、直线方程的不同形式间的关系直线方程的五种形式的比较如下表:
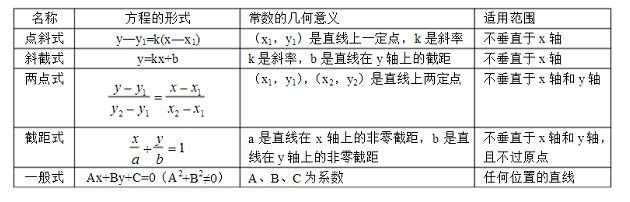
高中数学要点3、直线方程的综合应用
1.已知所求曲线是直线时,用待定系数法求.
2.依据题目所给条件,选择合适的直线方程的形式,求出直线方程.对于两直线的平行与垂直,直线方程的形式不同,考虑的方向也不同.
高中数学直线方程要点:表达方法
高中数学要点1:一般式:Ax+By+C=0(A、B不同时为0)
高中数学要点2:点斜式:y-y0=k(x-x0)
表示斜率为k,且过(x0,y0)的直线
高中数学要点3:截距式:x/a+y/b=1
表示与x轴、y轴相交,且x轴截距为a,y轴截距为b的直线
高中数学要点4:斜截式:y=kx+b
表示斜率为k且y轴截距为b的直线
高中数学要点5:两点式:
表示过(x1,y1)和(x2,y2)的直线
(y-y1)/(y2-y1)=(x-x1)/(x2-x1) (x1x2,y1y2)
高中数学要点6:交点式:f1(x,y) *m+f2(x,y)=0
表示过直线f1(x,y)=0与直线f2(x,y)=0的交点的直线
高中数学要点7:点平式:f(x,y) -f(x0,y0)=0
表示过点(x0,y0)且与直线f(x,y)=0平行的直线
高中数学要点8:法线式:xcosplay+ysin-p=0
过原点向直线做一条的垂线段,该垂线段所在直线的倾斜角为,p是该线段的长度
高中数学要点9:点向式:(x-x0)/u=(y-y0)/v (u0,v0)
表示过点(x0,y0)且方向向量为(u,v )的直线
高中数学要点10:法向式:a(x-x0)+b(y-y0)=0
表示过点(x0,y0)且与向量(a,b)垂直的直线


